Rotor-Stator Mixers: From Batch to Continuous Mode of Operation—A Review (3)

6. Implications for Emulsification
From an industrial perspective, the most important question with regards transitioning from batch to continuous RSM is how to operate a continuous mode RSM in a way such that it results in the same product quality as batch RSM. In an emulsification context, this corresponds to the question of how to predict the resulting drop diameters in batch and continuous operation RSMs, and to the question of whether there are mechanistic differences between the two products.

Turbulent drop breakup is often explained in terms of Kolmogorov–Hinze theory, which suggests scaling relations between the largest drop diameter that can survive a given turbulent field and the dissipation rate of TKE of that field. Depending on the size of this limiting drop in relation to the size of the smallest turbulent structures (the Kolmogorov length-scale), different explicit scaling laws have been suggested, see References for comprehensive reviews and some different explicit formulations.

However, as shown for impeller mixers and high-pressure homogenizers, in order for this approach to be satisfactory, the dissipation rate of turbulent kinetic energy should be the local value in the most intense region (where breakup takes place). However, since the local dissipation rate of TKE is highly challenging to measure, practical application of Kolmogorov–Hinze theory to RSMs are often based on externally measurable quantities such as rotor speed, the total dissipation power (Pdiss), and the globally defined Reynolds and Weber numbers. The global Weber number is defined as:

where σ is the interfacial tension of the drop. The Kolmogorov–Hinze theory is very general, and not specific to design or mode of operation. However, there is some disagreement in the scientific literature when it comes to the question of if there are mechanistic differences between emulsification in the two modes of operation, and hence, if the same scaling law expressions can be used for both modes of operation.

Experimental studies have reported some systematic differences. Emulsions passed n times through a batch RSM do not always show the same drop size as an emulsion processed for a time t = nτ, despite the fact that this would result in the same the number of passages though the RSM, at least in terms of expectation number. Three different standpoints discussing this discrepancy and the emulsification implications can be found in the RSM literature.

6.1. Flowrate and Its Influence on Turbulence
As previously mentioned, there is a decisive difference in flowrate (and thus in NQ) between RSMs operated in batch and continuous mode; batch mode RSMs show approximately ten times higher flowrates (Table 2). The difference between the two systems can be investigated by understanding the effect of flowrate on emulsification. Hall et al. undertook a large systematic investigation of emulsification in continuous mode RSMs and suggested that the flowrate-based Reynold number:

where d is the slot diameter and Atot is the total flow-through area of the stator, has a small but significant effect on the resulting drop size (when tip-speed is kept constant). When keeping the geometry constant, it can be shown that ReQ is proportional to the product between flow number and Reynolds number:

This would suggest that NQRe would be an appropriate scaling law when comparing emulsification results from batch to inline mode of operation. However, it should be kept in mind that the variations in flowrate seen in this type of experiment are much smaller than that between continuous and batch RSMs.

6.2. Radial Flow and Dissiaption Profile Scaling
RSM mixing and emulsification ultimately depends on the hydrodynamic conditions created in the rotor-stator region. Thus, it is interesting to investigate if there are any differences to the flow fields between batch and continuous modes of operation for the same rotor speed and rotor-stator head geometry. Unfortunately, no such experimental studies have been reported. However, a recent CFD investigation might be used to shed some light on the situation. The study reports flow fields obtained with CFD for a continuous mode RSM run at different flowrates and rotor speeds. The lower flowrates correspond to those generally obtained for continuous mode of operation (NQ = 0.007) and the higher to those obtained in batch mode of operation (NQ = 0.082). The radial velocity profiles in the stator holes were compared and it was found that neither ReQ nor NQReQ were appropriate scaling laws, in contrast to what was suggested in Section 6.1. Instead, it was found that both radial and tangential velocities (appropriately scaled with rotor speed) were determined by the flow number. This has an important implication on the difference between the two modes of operation. Since transitioning from batch RSM to a continuous mode RSM decreases NQ, the velocity profile in the rotor-stator head will undergo a substantial change. This change is not merely a scaling due to the reduction in flowrate but a shift into a fundamentally different turbulent flow. Most notably the position of the highest local dissipation rate of TKE shifts from the turbulent jet formed downstream of the slot in the batch RSM flow number, to the rotor-stator clearance for the continuous RSM flow numbers. This effect is illustrated in Figure 6.

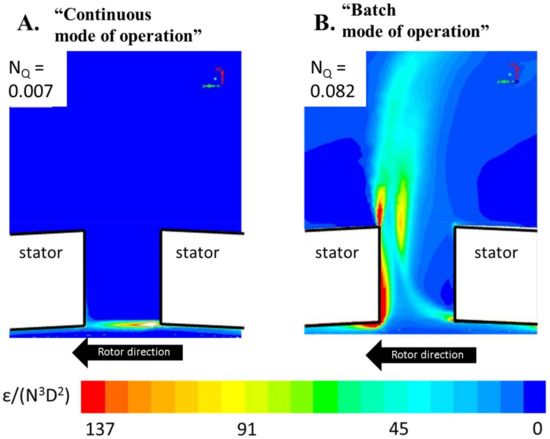
Figure 6. CFD-estimated dissipation rates of turbulent kinetic energy TKE in the stator slot region for the same rotor-stator head run at a flow number corresponding to an RSM run under continuous mode of operation (A) and run under batch mode of operation (B). Adapted from data obtained in Reference.

A shift in the position of highest local dissipation rate of TKE suggests a mechanistic difference between the two modes of operation. As seen in Figure 6, the dissipation volume is smaller for the low-NQ (continuous mode) case than in the high-NQ (batch mode) case. This also suggests that the average dissipation rate in the two regions will scale with different parameters: with the clearance length-scale for continuous RSMs and with the slot diameter for the batch RSM. However, this has not yet been experimentally verified.

Due to the lack of experimentally measured flow fields, this difference in flow pattern between modes of operation has not yet been experimentally verified, but a validation study has shown that the CFD model employed is able to capture the position of high intensity local dissipation at least for the batch RSM.

Further insight can be obtained by single drop breakup visualizations. However, only one such study on RSMs has yet been reported. This study was conducted for a batch RSM (NQ = 0.11) and showed that drops are deformed and subsequently broken up just downstream of the stator hole, as suggested by the CFD simulations for the NQ-values found in batch RSM (i.e., in Figure 6). However, no corresponding investigations on continuous RSMs (or low NQ-systems) have yet been reported.

6.3. A Purely Stochastic Effect
An altogether different, but highly promising approach to describe the previously reported differences between batch and continuous modes of operation on emulsification results has recently been reported. Carrillo De Hert and Rodgers suggest that the differences only apply if the wrong scaling is employed when comparing data from different modes of operation.

In the first step of their study, they conclude that the mode drop diameter, d0, resulting from processing an emulsion n times through their continuous mode RSM at flowrate Q and rotor speed N is given by:

Note the −6/5 exponent, that corresponds to the scaling expected from Kolmogorov–Hinze breakup in the turbulent viscous regime.

The authors then continue by suggesting that the only difference between continuous and batch modes of operation is in the stochastic effect of the rotor-stator head passage. After processing an emulsion for a time t in a batch system, the expectation number of the number of passages is:

However, for each volume element of the emulsion, the actual number of passages is a stochastic property following a Poisson distribution. By assuming that Equation (16) (the model for continuous mode of operation) applies each time a volume element passes the rotor-stator head, they conclude that the corresponding model for a batch system after being processed for a time t would be:

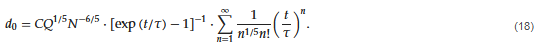
Moreover, for t/τ > 2, Equation (18) converges to:

which was found to accurately describe their data for a wide range of properties.

These results suggest that there is no mechanistic difference between the modes of operation and that (at least when processing times are fairly large) emulsification results can be translated directly using Equation (17); one continuous mode RSM passage would then correspond directly to processing for t/τ in a batch RSM. However, this is not completely general. In a previous study on emulsification of mayonnaise, it was concluded that this scaling was inadequate to describe the experimental differences. The reason behind this discrepancy is still not understood, but it is hypothesized that it is related to the higher volume fraction of oil in Reference which increases the complexity of the process.

In summary, there is as of yet no consensus in literature on which (if any) of these theories (Section 6.1, Section 6.2 and Section 6.3) best describes the differences between emulsification efficiency in batch and continuous modes of operation. Some of the confusion can be explained by postulating that the underlying differences between batch and continuous modes—i.e., the higher flowrate in batch systems—are the different hydrodynamic effects of the rotor-stator head in RSMs with different designs. It might be that the ReQ-scaling is appropriate for the design investigated by Hall et al. (a pilot scale Silverson dual blade design), that the NQ-scaling is appropriate for the design investigated by Håkansson et al. (a production scale Tetra Pak blade design), and that there is no mechanistic difference for the design investigated by Carrillo De Hert and Rodgers (a laboratory scale Silverson blade design). However, it is not clear why these different behaviors would occur, and how they could be linked to the design differences. Further investigations are needed in order to draw any definite conclusions on this matter.

7. Suggestion for Further Research
During the last couple of years, significant advances have been made into improving the fundamental understanding of RSMs in general and more specifically on the difference between batch and continuous modes of operation. However, there are still a number of issues that need further investigation, especially when it comes to the difference between continuous and batch modes of operation:

• Although general models for the scaling of power draw with operating parameters have now been obtained for both modes of operation (Equations (1) and (3)), there is still a lack of systematic investigation into how the model parameters (NP, NP0, NP1) depend on the design parameters (rotor, stator and tank dimensions). A better understanding of this would be helpful in the mechanical design of both batch and continuous mode RSMs.

• As seen throughout this review, the continuous mode RSM could be seen as something between a batch RSM and a centrifugal pump. Further investigations on the relative pumping and turbulence producing properties of different mixer designs (i.e., determination of pumping constants, c1 and c2) would be helpful for choosing the right rotor-stator head for a given application.

• A large number of experimental studies correlating drop sizes to operating parameters have been published, but it has been difficult to use these studies to obtain a fundamental understanding of the breakup process or the underlying hydrodynamics of RSMs. The single drop breakup visualizations reported by Ashar et al. shows a promising alternative approach where the breakup probabilities are measured directly and then linked to the local hydrodynamic conditions. Expanding these types of investigations into other RSM geometries and repeating it for a continuous mode RSM is needed to further our fundamental understanding.

• As seen in Section 6, there is some remaining uncertainty whether there exist mechanistic differences between breakup when using the same rotor-stator head in the batch or continuous mode of operation. Comparing the scaling suggested by Carrillo De Hert and Rodgers to data from more RSM designs could be one way towards reaching a more definite conclusion; single drop breakup visualization in a continuous mode RSM at varying NQ-values would be another interesting way forward.

8. Summary and Conclusions
The objective of this contribution was to review the current scientific based understanding of the differences between RSMs in batch or continuous mode of operation. Section 3 showed that correlations for shaft power draw are available for both modes of operation, allowing for accurate prediction of process economy in terms of energy expenditure. In Section 4, it was seen that the flow number (NQ), and consequently the flow through the stator screen, Q, is considerably lower for continuous mode of operation (compared to batch mode) when using the same rotor-stator head and operating it at the same rotor speed. Section 5 showed that, in general, a much higher proportion of the energy fed to the shaft is converted into turbulence in the high-intensity region where mixing and emulsification takes place for a batch RSM than for an RSM operated in continuous mode. For a continuous mode RSM, more of the energy is used for pumping (i.e., increasing the head of the flow). Section 6 discussed what this implies when comparing emulsification efficiencies between the two modes of operation. Several different theories have been suggested, but there is of yet no clear consensus in the literature for how continuous mode RSMs should be operated in order to give the same emulsion as in a batch RSM.

Håkansson, A. Rotor-Stator Mixers: From Batch to Continuous Mode of Operation—A Review. Processes, 6(4), 32. https://doi.org/10.3390/pr6040032

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).