Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM) （1）
1. Introduction
Mixing of granular materials is a common practice in many industries such as the food, pharmaceutical and chemical industry, where consistent product quality is of great importance and is highly desirable. Mixing can be performed utilising gravity-controlled, high-shear or agitated mixers, which are highly popular because of their ability to handle a wide range of operational tasks. Agitated mixers can be in the form of single or double vessels in the horizontal or vertical direction. Taking the shape of the agitators into account, they can be classified into paddle, ploughshare, ribbon and screw blenders.
Several experimental studies have investigated agitated mixers by measuring the required force and torque for mixing, or by using positron emission particle tracking (PEPT) and particle image velocimetry (PIV) to characterise particle flows. Although these experimental investigations have provided valuable insights into the mixing process, they were constrained to a limited number of particle properties or operational parameters. Moreover, obtaining local information on particle velocity and forces, which can shed light on the mixing mechanisms, is nearly impossible in experiments.
The discrete element method (DEM), initially introduced by Cundall and Strack, is a powerful tool which can provide detailed information on the particle level. Additionally, the influence of various types of parameters affecting the mixer's performance can be examined efficiently using DEM. Due to these advantages, DEM has been extensively utilised to study various types of agitated mixers including single vessel mand double vessel mixers.
However, there are very few DEM studies concerning the mixing performance of double paddle mixers, which is a type of agitated double vessel mixer. Jadidi et al. have investigated the mixing performance of a double-shaft, paddle mixer by performed a sensitivity analysis on the impeller speed, initial loading pattern and fill level. First, they calibrated the DEM model for mono-disperse particles of 5 mm. The calibrated model was then used to study the mixing behaviour of particles with different colours (but the same size). It was concluded that the impeller rotational speed and the initial loading pattern had a significant effect on the mixing performance. Nevertheless, the fill level did not significantly affect the mixing performance. Moreover, using response surface methodology (RSM), they revealed that the interaction between the operating parameters did not significantly affect the mixing performance. As a follow-up study, Jadidi et al. also investigated the effect of bi-disperse spherical particles, besides the impeller rotational speed and fill level, using both experiments and DEM simulations. It was found that the impeller rotational speed and the particle number ratio had a significant effect on the mixing performance. That is, a higher rotational speed and a higher number ratio resulted in an improved degree of mixture homogeneity, irrespective of the fill level. Recently, Jadidi et al. investigated the effect of non-spherical particles on the mixing performance of the double-shaft paddle mixer. They concluded that particle shape can significantly influence the mixing performance, since non-spherical particles showed higher bed compactness and higher resistance to movement. Hence, the mixer exhibited the best performance, i.e., the lowest relative standard deviation (RSD) mixing index, for spherical particles. Furthermore, Jadidi et al. suggested to further investigate the effect of the size and density of the materials.
Despite the mentioned attempts, it is not yet well understood how the mixing performance of double paddle mixers is affected by parameters other than the ones related to material or operational conditions. This study aims to gain knowledge about the parameter's significance by investigating not only the effect of material properties (i.e., size ratio, density ratio and composition) and operational conditions (i.e., initial filling pattern, fill level and impeller rotational speed), but also the geometric parameters (i.e., paddle size, paddle angle and paddle number) on the mixing performance using DEM. Four key performance indicators (KPIs), namely the mixing quality, mixing time, average mixing power and total energy consumption to reach a saturated mixing quality, were defined to lead towards a deeper understanding of the mixer performance. The KPIs related to energy were adjusted to account for the granular mass in the mixer. Using a statistical design of experiment (DoE) approach (i.e., Plackett–Burman), the factors that significantly influence each KPI were determined. Furthermore, the time-averaged granular temperatures in three different locations were calculated to spatially explore the mixing diffusivity. The results can be used to further optimise the performance of double paddle mixers.
2. Materials and Methods
2.1 Modelling Approach
The discrete element method (DEM) was utilised to simulate the mixing mechanisms and flow patterns inside the paddle mixer. The methods in relation to mixing operations have been successfully employed in many areas such as agricultural technology, chemical engineering, pharmaceutical industry, food industry and process engineering .
Considering the soft-sphere method, particles experience two types of motions during simulation: rotational and translational. Both are governed by Newton’s laws of motion. The forces and torques on an individual particle are caused by interaction with other particles or the system's boundaries. In Equations (1) and (2), the translational and rotational equations of motion are formulated.
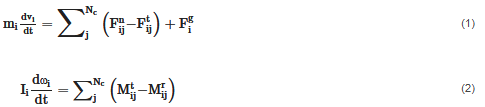
where mi, vi and ωi are the mass, translational velocity and angular velocity of the individual particle I, respectively. The variables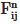 
and
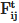are the normal and tangential components, respectively, of the contact force between particle i and particle j and 
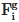represents the gravitational force on particle i. Variables
are the moment of inertia, rotational torque and rolling resistance torque between particle i and particle j, respectively. The coordination number Nc represents the number of particles in contact with particle i.
In this study, the two mixture components consist of free-flowing spherical particles to minimize the computational expense. The Hertz–Mindlin contact model is used to model the interactions between the particles and the interactions between particles and geometry. This model is most suitable since it takes into account the nonlinear elastic contact behaviour of particle–particle and particle–geometry interactions. Normal and tangential contact forces are calculated by Equations (3) and (4).
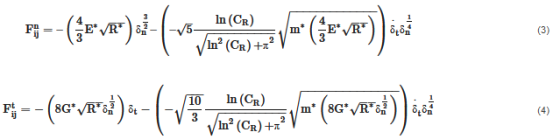
where CR, δn and δt are the coefficient of restitution, the normal overlap and the tangential overlap, respectively. The symbols E*, R*, m* and G* are the equivalent Young's modulus, the equivalent radius, the equivalent mass and the equivalent shear modulus, respectively, calculated by Equations (5)–(8).
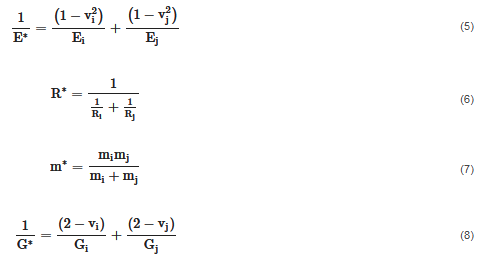
where Ei, Ri, mi, Gi and vi are the Young's modulus, the radius, the mass, the shear modulus and the Poisson's ratio of particle I, respectively.
In this study, Altair EDEM was used as the DEM solver. The simulations were conducted in parallel mode using 28 CPUs and 1 GPU of a high-performance computer (Intel(R) Xeon(R) W-2275 CPU @ 3.30GHz, 16GB RAM). Post-processing was performed using Python v3.9.12 in IDE Spyder v5 and Altair’s HyperStudy v2022.1.
2.2 Simulation Setup
The 175 L double shaft, batch-type paddle mixer (Figure 1a) is based upon the first design by Forberg. The shafts are positioned horizontally, each equipped with 14 paddles that are evenly distributed over four radial quadrants. The paddles are configured in such a way that they force the granular material in the radial direction (to the centre of the mixing chamber) and in the axial direction (to move in a circular pattern through the chamber).
Figure 1. (a) Isometric view, (b) front view and (c) side view of the paddle mixer. For clarity, only shaft 2 is shown in the side view.
To avoid accumulation in the corners of the mixing chamber, the last two paddles are positioned in the opposite direction with a 15 deg angle and serve as 'transfer' paddles (Figure 1a). To avoid collisions between the paddles of the two shafts, a phase angle of 45 deg is applied (Figure 1b). The dimensions of the mixing chamber are listed in Table 1. Detailed dimensions of the shaft and paddles are left out due to confidentiality reasons. The DEM input parameters of this study are listed in Table 2.
Table 1. Dimensions of the paddle mixer as shown in Figure 1.
Parameter | Unit | Value |
L | mm | 900 |
W | mm | 850 |
H | mm | 570 |
Table 2. Discrete element method (DEM) input parameters. The Poisson's ratio, νw, and the shear modulus, Gw, are adopted from.
Parameter | Unit | Value |
Poisson's ratio, νp | - | 0.3 |
Shear modulus, Gp | Pa | 1 × 106 |
Particle-particle coefficient of restitution, ep−p | - | 0.75 |
Particle-particle coefficient of static friction, μs, p−p | - | 0.5 |
Particle-particle coefficient of rolling friction, μr, p−p | - | 0.01 |
Geometry density, | kg m−3 | 7850 |
Poisson’s ratio, νw | - | 0.265 |
Shear modulus, Gw | Pa | 7.4 × 1010 |
Particle-geometry coefficient of restitution, ep−w | - | 0.75 |
Particle-geometry coefficient of static friction, μs, p−w | - | 0.35 |
Particle-geometry coefficient of rolling friction, μr, p−w | - | 0.005 |
Simulation time, t | s | 60 |
Time step, Δt | s | 4.74378 × 10−5 |
The article had to be closed because of word limit. Please look forward to the next news which will continue.
© 2023 by the authors.
Licensee MDPI, Basel, Switzerland. This article is an open access
article distributed under the terms and conditions of the Creative
Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
